Keras 入门教程
在深度学习领域中,一直有许多好用的框架,例如 TensorFlow、PyTorch、Theano 等。而在这一些框架之上, 也有一些较为“高级”的框架,例如 Keras、TensorLayer、TFLearn 等。相较于 TensorFlow 这样的基础框架,高级框架使模型的搭建变得更为便捷,并且隐藏了一些底层的原理。因此对于初学者而言,高级框架的代码会更直观,也更易于理解。 (但是这样不利于我们去了解模型背后的原理,因此我们也应该通过底层的框架去实现原理)。
而这一篇教程,主要介绍的是 Keras 这一个框架。实际上,这几个高级框架并没有太多的区别,不过相较于其他框架, Keras 的语法更具有 python 的风格,模型的结构也更为直观,并且它无论在初学者中还是研究领域都有着比较多的用户,因此这一篇教程将会围绕着 Keras 进行介绍。
这一篇教程将会介绍一些 Keras 常用的语句,并且将会教你搭建一个最简单的模型,用来识别手写数字。那么接下来,就从安装 Keras 开始。
0. 安装 Keras
照例,要使用 Keras 这一个模块,我们需要先安装它。因为 Keras 是一个高级框架,所以他还会同时安装 TensorFlow 作为它的后端。
pip install keras
或者,如果你使用 anaconda 。
conda install keras
如果之前安装过了 TensorFlow ,建议删除 TensorFlow 之后再安装 Keras ,不然可能会出现版本不兼容的问题。
安装完成之后,打开 python ,输入 import keras ,这时候应该会有以下提示:
>>> import keras
Using TensorFlow backend.
如果成功输出,就说明 Keras 已经安装成功了。
1. 了解数据集
在这一篇教程中,我们将要实现一个能够识别手写数字的模型。而为了训练这一个模型,我们需要用到 MNIST 数据集。
1.1 什么是 MNIST 数据集
MNIST 数据集是一个手写数字图像的数据集,它包含了 60,000 张训练用的图像,以及有 10,000 张测试图像。每一个数字图像都是 28x28 的,而下面是其中一部分的图像。

了解了什么是 MNIST 数据集之后,我们需要在代码中导入这个数据集。
1.2 Keras 导入 MNIST 数据集
正常情况下,我们需要将数据集的图片解压,然后再导入。不过好在 Keras 内部已经包含了 MNIST 数据集的导入操作,让我们看一下如何导入数据集:
from keras.datasets import mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()
load_data() 函数会返回两个元组,其中包括训练数据 (X_train, y_train) 和测试数据 (X_test, y_test) 。
在训练数据中, X_train 代表的是输入的图片,而 y_train 代表了标签 (这个图片对应的数字) 。让我们来看一下 X_train 和 y_train 的大小。
>>> X_train.shape
(60000, 28, 28)
>>> y_train.shape
(60000,)
可见,训练数据中总共有 60,000 个训练图片,每张图片都是 28 x 28 的大小。
在了解了数据集的输入和我们的目标了之后,接下来一步,我们需要先对数据进行预处理。
2. 对数据进行预处理
2.1 对 X_train 进行标准化
一般来说,我们都需要将输入进行标准化,使其分布于 [-1, 1] 或者是 [0, 1] 这样一个区间,从而便于网络进行学习。
对于我们这样一个数据集, X_train 中存储的是图像的像素灰度,因此它的值的范围为 0-255 ,我们需要将 X_train 进行标准化至 [-1, 1] ,公式如下:
这个公式转化为代码也十分简单,不过要记住先将其转化为浮点型再进行运算。
X_train = X_train.astype('float32') / 127.5 - 1
2.2 将 y_train 转为 One-Hot 编码
当输出 y_train 中的元素时,我们可以发现其中存储的是每一张图片对应的数字:
>>> y_train[:10]
array([5, 0, 4, 1, 9, 2, 1, 3, 1, 4], dtype=uint8)
这样的表示方法对于人而言很容易理解,但是这样不利于去训练我们的模型。可能大家会感到疑惑,为什么不能通过输出 0-9 来分类呢?
其实,这是因为这 10 个数字之间是没有相关性的。有一个很直观的假设是:假如输入了一个很像 3 的数字,那它应该输出什么呢?有可能这个网络就会输出 3.9 。所以我们不能用 0-9 这样的连续的数字去做分类,而应当使用 One-Hot 编码。
那什么是 One-Hot 编码呢?我们可以用一个公式来表示编码的过程:
\[encoded = \begin{bmatrix} a_1 & a_2 & a_3 & ... & a_n \end{bmatrix}\] \[a_i = 1 \ \ \ (i = y)\] \[a_i = 0 \ \ \ (i \neq y)\]直接看公式可能会比较费解,那就使用手写数字分类的问题来举例吧。对于这个问题来说,将 y_train 转化为 One-Hot 编码后,它就会变成其中一项概率为 1 ,其余都为 0 的情况。例如,数字 2 的 One-Hot 编码将会是 [0, 0, 1, 0, 0, 0, 0, 0, 0, 0] 。这样模型在预测时,就可以将这个问题转化为分类的问题,如果它觉得是某一类的概率更高,那么对应位置的数值就会变大。
那么,如何将 y_train 转化为 One-Hot 编码的? 哈哈,这个 Keras 中也已经为我们准备好了:
from keras.utils import to_categorical
y_train = to_categorical(y_train)
只需要调用 keras.utils.to_categorical 函数,我们就能实现 One-Hot 编码的转化。
完成了标准化和 One-Hot 编码后,我们就完成了对数据的预处理,接下来我们将要设计一个模型结构,并用处理后的数据对其进行训练。
3. 设计多层感知器模型
作为最入门级别的教程,我们就先设计一个最基本的多层感知器结构。不过在实现这样一个网络之前,我们需要先介绍一些神经网络的基础知识。
3.1 人工神经元模型
人工神经元,是神经网络的基础。
在生物学中,一个神经元的模型大约是下图所示:
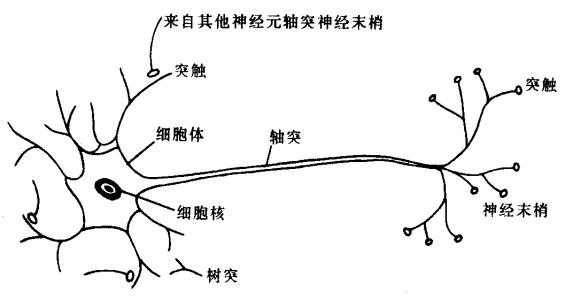
而人工神经元模拟了生物神经元的机理,将其抽象为下面所示的数学模型:
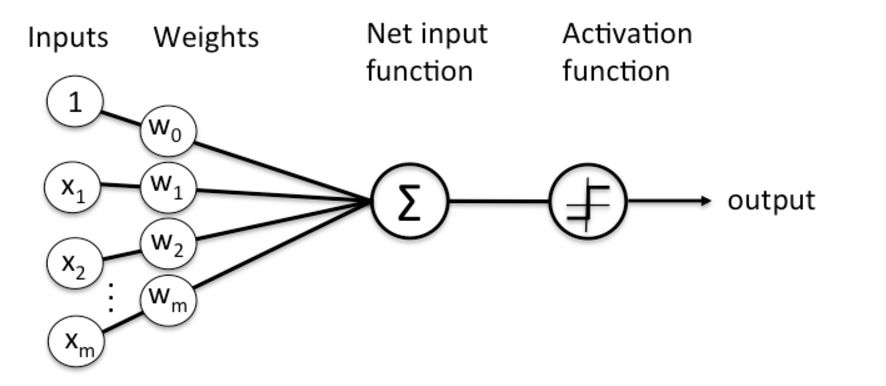
如果将其写成公式,可以表达为以下的形式:
\[output = activation(\sum _{i = 1} ^n w_i x_i + b)\]我们也可以将其改写为向量形式:
\[W = \begin{bmatrix} w_1 \\ w_2 \\ ... \\ w_n \end{bmatrix} \ \ \ X = \begin{bmatrix} x_1 \\ x_2 \\ ... \\ x_n \end{bmatrix}\] \[output = activation(W^T \cdot X + b)\]可以看到,人工神经元正是模拟了生物神经元接受外界刺激,并产生信号的过程。而将多个人工神经元组合在一起,我们就能够得到一个人工神经网络。
3.2 多层感知器网络
将多个人工神经元组合在一起,就可以得到一个层。如果两层之间的所有神经元都是连接的,那么这个层就叫做全连接层。
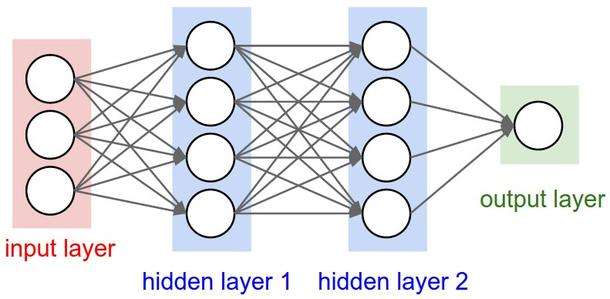
在上文中,我们可已经得到了一个人工神经元的输入输出公式,那么,通过这个公式我们就可以得到两层全连接层的公式,这里以上图所示的第一层 (hidden layer 1) 的计算为例:
首先,输入的向量为 $X_1$ ,维度为 3 :
\[X_1 = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}\]在两层之间,有权重矩阵 $W_{1,2}$ 和偏置向量 $B_{1,2}$ :
\[W_{1,2} = \begin{bmatrix} w_{11} & w_{12} & w_{13} & w_{14} \\ w_{21} & w_{22} & w_{23} & w_{24} \\ w_{31} & w_{32} & w_{33} & w_{34} \end{bmatrix} \ \ \ B_{1,2} = \begin{bmatrix} b_1 \\ b_2 \\ b_3 \\ b_4 \end{bmatrix}\]那么,我们得到的输出 $X_2$ 的计算公式是:
\[X_2 = activation(W ^T _{1,2} \cdot X_1 + B_{1,2})\]这样,我们就可以使用向量点积得到输入向量通过一层全连接层之后的输出结果了。
而许多全连接层组合在一起,我们就能得到一个多层感知器 (Multi-Layer Perceptron, MLP) 。根据这些层的位置,我们可以将它们分为输入层、隐藏层、输出层。其中,输入层的大小需要和输入数据的大小相同,输出层的大小需要和最终分类所需的种类个数一致。而隐藏层的层数以及每一层的大小都可以自由设置。
3.3 实现一个多层感知器
了解了多层感知器模型后,我们需要针对当前的问题,去设计一个模型。
对于现在的识别手写数字问题,我们输入的数据大小为 28x28 = 784 ,而最终我们需要将它分为 10 类。因此 输入层的大小为 784 ,而输出层的大小为 10 。为了将最终的结果变为概率分布,我们需要在最后一层使用 softmax 函数。限于篇幅,这里不介绍这个激活函数的原理。
接下来确定隐藏层,为了简化,我们只设计一层隐藏层,并且将其大小设为 100 (隐藏层的大小完全可以自由设置,不一定要完全按照教程) 。于是,我们的多层感知器就设计完成了:
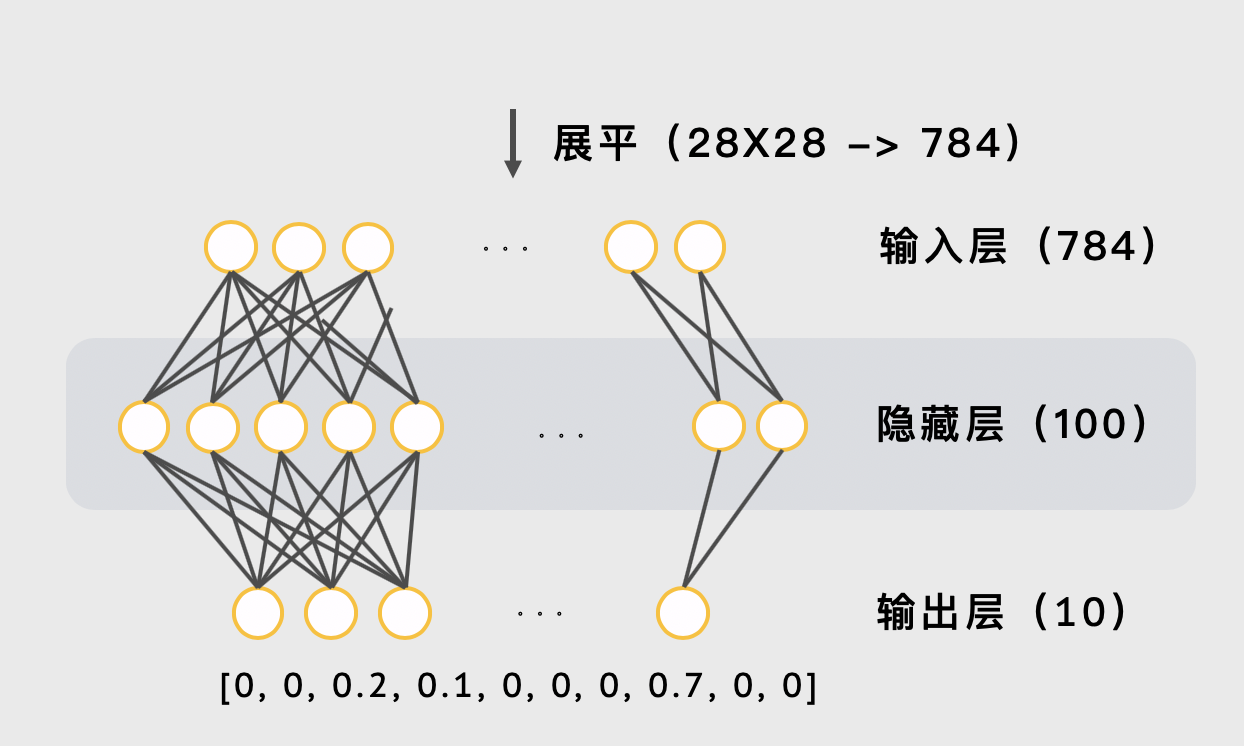
模型的一开始使用了一个展平层,这是因为我们的输入是一张 28x28 的图像,而如果要用于多层感知器,我们需要先使用展平层将其展成一个向量。
4. 编写模型
设计完了模型,我们就可以用代码来编写它了。在这里就会体现出 Keras 的一大优点:代码非常简洁,并且可读性很高。让我们直接来看代码:
from keras.models import Sequential
from keras.layers import Flatten, Dense
model = Sequential([
Flatten(input_shape=(28, 28)),
Dense(units=784,
activation='relu'),
Dense(units=100,
activation='relu'),
Dense(units=10,
activation='softmax')
])
这里我们定义了一个序列 (Sequential) 模型,其中第一层 Flatten 就是展平层,它有一个参数 input_shape ,代表着输入的大小。我们的输入为 28x28 的图片,因此设置 input_shape=(28, 28) 。
后面三层 Dense (全连接层) 就分别代表了我们的输入层、隐藏层和输出层。 units 参数设置了每一层的单元个数,分别为 784 、 100 和 10 。而 activation 参数设置了每一层的的激活函数。可以看到,我们在前两层使用了 relu (修正线性单元) 函数,而在最后一层使用了 softmax 函数,输出概率分布。关于这两个激活函数,大家可以自行搜索它们的原理。
由此,我们的模型就编写完了。编写完成后,使用 model.summary() 这一个方法就可以返回模型的结构。从而我们就可以用 print 输出出来:
# 输出模型结构
print(model.summary())
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten_1 (Flatten) (None, 784) 0
_________________________________________________________________
dense_1 (Dense) (None, 784) 615440
_________________________________________________________________
dense_2 (Dense) (None, 100) 78500
_________________________________________________________________
dense_3 (Dense) (None, 10) 1010
=================================================================
Total params: 694,950
Trainable params: 694,950
Non-trainable params: 0
_________________________________________________________________
None
5. 编译并训练模型
定义完了模型结构,并且准备好了数据,接下来我们就可以对模型进行训练了!
首先,我们先用 compile 设置模型的其他参数。为了训练一个模型,我们需要设置优化器 (optimizer)、损失函数 (loss)、评估方法 (metrics) 这三个参数。 Keras 支持直接将优化器和损失函数对应的名称传入,这样会使用默认的参数。
model.compile(loss='mse',
optimizer='sgd',
metrics=['acc'])
在这里,我们选择使用均方误差 (Mean-Square Error, MSE) 来作为我们的损失函数,而采用随机梯度下降法 (Stochastic gradient descent, SGD) 来优化。关于优化器与损失函数的原理,这里不会详细介绍。
最后,我们使用 fit 方法,就可以对模型进行训练了:
# 训练模型
model.fit(x=X_train,
y=y_train,
validation_split=0.2,
epochs=10,
verbose=2)
首先我们传入了数据以及标签 x , y。而 epochs 参数代表模型要训练的轮数, verbose 参数设置了训练时的日志显示模式 (0 = 安静模式, 1 = 进度条, 2 = 每轮一行) 。而 validation_split=0.2 表示将 20% 的数据用于验证。那么验证又是什么呢?
在用于验证的数据中,我们只会评估准确率,不会对其进行训练。也就是说,验证数据集存放着这个模型没有学习过的样本,这样有利于我们去检测模型的适应程度。
运行这一段代码,在经过一段等待后,我们的模型就训练完成了。
Train on 48000 samples, validate on 12000 samples
Epoch 1/10
- 14s - loss: 0.0635 - acc: 0.5526 - val_loss: 0.0386 - val_acc: 0.8013
Epoch 2/10
- 12s - loss: 0.0315 - acc: 0.8277 - val_loss: 0.0245 - val_acc: 0.8638
Epoch 3/10
- 12s - loss: 0.0235 - acc: 0.8636 - val_loss: 0.0200 - val_acc: 0.8834
Epoch 4/10
- 12s - loss: 0.0202 - acc: 0.8803 - val_loss: 0.0177 - val_acc: 0.8932
Epoch 5/10
- 12s - loss: 0.0183 - acc: 0.8891 - val_loss: 0.0163 - val_acc: 0.9017
Epoch 6/10
- 13s - loss: 0.0170 - acc: 0.8959 - val_loss: 0.0153 - val_acc: 0.9065
Epoch 7/10
- 12s - loss: 0.0160 - acc: 0.9008 - val_loss: 0.0146 - val_acc: 0.9102
Epoch 8/10
- 13s - loss: 0.0153 - acc: 0.9050 - val_loss: 0.0140 - val_acc: 0.9133
Epoch 9/10
- 15s - loss: 0.0147 - acc: 0.9086 - val_loss: 0.0136 - val_acc: 0.9155
Epoch 10/10
- 13s - loss: 0.0142 - acc: 0.9121 - val_loss: 0.0131 - val_acc: 0.9181
可以看到,我们的模型在训练集中的准确率有 91.21% ,而在评估集中有 91.81% 。说明比起随机猜测来说,模型已经学习到了一定的特征。不过对于识别手写数字这样的一个简单的问题而言,十个里面错一个的准确率还是比较低的。
主要的原因还是在于模型结构。多层感知器的结构并不适合处理图像一类的数据,而在下一个教程中,我们将会介绍如何使用 卷积神经网络 (Convolutional Neural Networks, CNN) 来提升模型的准确率。
结语
通过这样一个简短的教程,我们稍微了解了一些 Keras 中的内容,并且自己搭建了一个简单的网络来完成手写数字的识别。不过限于篇幅,文章中没有介绍激活函数、损失函数、优化器的原理,因此也希望大家能够在其他博客中了解一下这些内容。
此外,关于更多的 Keras 用法,也可以去学习它的官方文档:Keras.io/zh/ 。
附:程序的完整代码
from keras.utils import to_categorical
from keras.models import Sequential
from keras.layers import Flatten, Dense
from keras.datasets import mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train = X_train.astype('float32') / 127.5 - 1
y_train = to_categorical(y_train)
model = Sequential([
Flatten(input_shape=(28, 28)),
Dense(units=784,
activation='relu'),
Dense(units=100,
activation='relu'),
Dense(units=10,
activation='softmax')
])
# 输出模型结构
print(model.summary())
# 编译模型
model.compile(loss='mse',
optimizer='sgd',
metrics=['acc'])
# 训练模型
model.fit(x=X_train,
y=y_train,
validation_split=0.2,
epochs=10,
verbose=2)