[ML] 数据降维与可视化算法

数据降维，指的是通过某种映射，将高维的数据转换为低维。通过数据降维，我们能够在保持原数据信息损失不大的情况下，将数据压缩存储，从而降低空间消耗。在机器学习或是数据科学的任务中，我们往往需要将样本点的分布进行一定的可视化。然而，超过三维的数据往往就很难做可视化的处理，此时我们可以使用数据降维算法，将样本变为二维/三维空间上的点，从而能够非常直观地进行绘制与展示。

常见的数据降维算法主要有主成分分析以及 t-SNE 算法，而主成分分析又有特征分解以及奇异值分解两种做法。在接下来的博客里，我将会简单介绍这三种常见算法的原理、公式以及算法流程，在最后，我也会进行一定地总结与分析。

1. PCA (Principal Component Analysis, 主成分分析)

主成分分析是一种非常简单线性降维方法，其理论基础是最大方差定理。

1.1 最大方差定理

最大方差定理指出，为了尽可能保留样本的信息，我们需要选择样本投影方差最大的方向作为新的基。

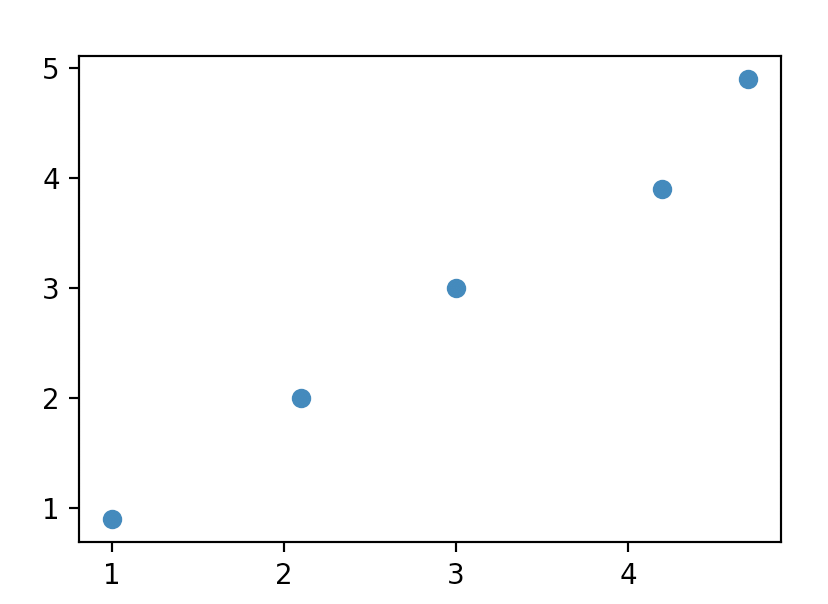
举个例子，例如在二维平面上有下面五个样本：

将其绘制出来如下图所示：

此时，投影后方差最大的单位方向向量为

取与 $p_1$ 正交的单位方向向量 $p_2$ ：

把两个向量画在图中：

不难发现，这些样本基本上都是沿着 $p_1$ 方向分布，而在 $p_2$ 方向只有较少的变化，因此我们可以忽略 $p_2$ 方向的变化，将所有样本点投影至 $p_1$ 方向，从而就能够将二维数据压缩成一维数据。因为 $p_1$ 为单位向量，因此投影即为向量内积。最后我们得到的结果为：

在这个例子中，我们仅仅只是选取了一个最大方差的方向作为新的基。而如果要将 $m$ 维数据降维到 $k$ 维，我们则需要选取 $k$ 个正交的方向，使得样本在这 $k$ 个方向投影后的方差最大，就能尽可能保留数据的信息。

1.2 特征分解

虽然通过最大方差定理就能够对数据进行降维，但是有一个新的问题：如何找到最优的 $k$ 个投影方向？在 PCA 中，这 $k$ 个方向即为样本协方差矩阵最大的 $k$ 个特征值所对应的特征向量。为什么是这样？接下来将进行简单的证明：

首先，记样本 $X$ 为：

其中，每个样本 $x_i$ 均为 $m$ 维的列向量。接下来求样本的协方差矩阵：

其中，$\overline x$ 为 $x$ 的均值。接下来我们假设投影矩阵为 $P$ ，$P$ 是幺正矩阵，即：

投影后的结果为 $Z = P^T X, z_i = P^T x_i$ 。

此时，我们将投影后的样本 $Z$ 的协方差表示出来：

由于均值的性质，我们很容易得到：

由此，我们可以将 $Z$ 的协方差用 $P$ 和 $X$ 表示：

通过化简，我们会发现，$Z$ 的协方差矩阵与 $X$ 的协方差矩阵有非常直接的关系。并且对于 $Cov(Z)$ ，对角线上的元素即代表方差，对角线外的元素则代表维度间的协方差。

取 $Cov(Z)$ 对角线上的第 $i$ 个元素，记为 $\sigma_i^2$ ，则满足：

此时 $\sigma_i^2$ 即为投影后的方差。为了使方差最大（即使 $\sigma_i^2$ 最大），并且满足约束，可以构造拉格朗日函数：

对 $p_i$ 求导，并令导数为 $0$ ，可得：

即 $\lambda_i$ 为 $Cov(X)$ 的特征值， $p_i$ 为 $\lambda_i$ 对应的特征向量。

首先进行检验：因为 $Cov(X)$ 是实对称的，因此其必定能够进行特征分解。由此，我们可得：

因此，当取 $\lambda_1, \lambda_2, …, \lambda_k$ 为最大的 $k$ 个特征值时，得到的方差最大，此时 $e_1, e_2, …, e_k$ 为对应的 $k$ 个特征向量。证明完毕。

1.3 PCA 的算法过程

了解了 PCA 的公式原理之后，实现这个算法就非常容易了，大概可以分为下面几个步骤：

1. 求原始数据的协方差矩阵
2. 求协方差矩阵的特征值与特征向量，并进行排序
3. 取前 $k$ 大特征值对应的特征向量，或是舍弃一定阈值下特征值对应的特征向量，组成投影矩阵
4. 通过投影矩阵求得降维后的结果

使用 numpy 实现 PCA 也非常容易：

def PCA(X, k):
    cov = np.cov(X)
    w, V = np.linalg.eig(cov)
    index = np.argsort(w)
    P = V[:,index[-k:]]
    Z = np.dot(P.T, X)

    return Z

2. PCA-SVD

除了对样本的协方差矩阵进行特征分解外，我们还可以引入奇异值分解 (Singular Value Decomposition, SVD) 的方法，来做主成分分析的运算。

2.1 SVD 的定义

当一个矩阵 $A$ 为 $n \times n$ 的实对称矩阵时，我们能够对其进行特征分解，即：

其中：

而当矩阵 $A$ 不为方阵时，就可以使用奇异值分解。当 $A$ 为 $m \times n$ 时，其分解形式为：

此时，$U$ 的大小为 $m \times m$ ，$V$ 为 $n \times n$ ，他们都为幺正矩阵，且 $U$ 由 $A A^T$ 的特征向量构成，$V$ 由 $A^T A$ 的特征向量构成，即：

而 $S$ 的大小为 $m \times n$ ，其对角线外的元素均为 $0$ ，而对角线上的元素即成为奇异值，记为 $\sigma$ 。

2.2 SVD 与特征分解

在计算 PCA 时，我们需要对 $Cov(X)$ 进行特征分解，求出其特征值与特征向量，才能求得我们所需要的投影矩阵，即：

对样本 $X$ 进行均值归一化，得到矩阵 $Y$ ，即：

那么不难证明：

如果对 $Y$ 进行奇异值分解，则可以得到（为了不与上文的 $V$ 混淆，这里用 $V_y$ 作区分）：

将其带入 $X$ 的协方差中，则可得：

由于 $V_y^T V_y = I_n$ ，所以：

因为奇异值分解中的 $U$ 矩阵即为 $Y Y^T$ 的特征向量构成的矩阵，所以我们可以知道：

也就是说，对均值归一化的 $Y$ 矩阵进行奇异值分解，我们同样也能得到 $Cov(X)$ 的特征值与特征向量。

2.3 PCA-SVD 的算法过程

PCA-SVD 的算法过程非常简单，也只需要四步：

1. 求出样本均值归一化后的矩阵
2. 对其进行奇异值分解
3. 选出前 $k$ 大奇异值所对应的左奇异矩阵对应的列向量，组成投影矩阵
4. 通过投影矩阵求得降维后的结果

numpy 中已经为我们实现了 SVD 的求解算法，因此代码也非常容易：

def PCA_SVD(X, k):
    Y = X - np.mean(X, axis=1, keepdims=True)
    U, s, V = np.linalg.svd(Y)
    index = np.argsort(s)
    P = U[:,index[-k:]]
    Z = np.dot(P.T, X)

    return Z

2.4 SVD 的优势

那么，相对于使用特征分解进行主成分分析，SVD 有什么优势呢？

有些人说：特征分解只对实对称矩阵有效，而 SVD 可以对非方阵分解。首先，没错，这的确是 SVD 相较于特征分解的优势，但是在 PCA 算法中这并不是问题。如果你没有忘的话， PCA 是对样本 $X$ 的协方差矩阵 $Cov(X)$ 进行特征分解，而协方差矩阵一定是实对称的，必定可以特征分解。因此这并不是问题。

也有很多资料说：SVD 不需要对协方差矩阵进行计算，只需要对样本进行分解即可。非常明显，这也是一个错误的结论。首先，SVD 需要将矩阵 $Y$ 分解成三个部分：

而矩阵 $U$ 的求法，就是求出 $Y Y^T$ 的特征向量，而协方差矩阵为 $Cov(X) = \frac1{n - 1} Y Y^T$ 。对这两个矩阵进行分解，实际上是等价的。

那么，难道是因为 SVD 有特殊算法，会让运算速度加快吗？通过随机生成矩阵，用 numpy 进行测试，我发现 SVD 算法的平均时间是特征分解方法的两倍以上，也就是说，在速度上，SVD 算法也没有优势。

那么，到底为什么要用 SVD 算法呢？其实在数学意义上，PCA 可以用的场景 SVD 也都可以用，此时，他们在数学意义上是等价的。

然而，在计算机具体的实现上（数值分析意义下），PCA 和 SVD 都需要进行特征值分解。根据 Abel-Ruffini 定理，5 阶及以上的特征多项式都没有闭式解，即此时计算特征值只能使用相似方法（会有误差），而 PCA 直接使用了这样（带有误差的）特征值，但 SVD（简单讲）会使用特征值的根，因此对于数值分析意义上的误差，SVD 的鲁棒性比 PCA 更高。

一句话来讲，当进行主成分分析时，SVD 在数值分析意义下比特征分解更稳定。

更多信息可以参考 NYU 的 Lecture

3. t-SNE

上文介绍了两种降维的方法均是线性的，然而在很多时候样本之间的分布都是非线性的。此时，如果我们要对样本进行可视化（降维至三维及以下），使用线性的降维方法可能无法很好地区分开不同样本，此时我们就需要使用非线性的降维算法。

t-SNE 就是解决这个问题的一个很好的算法，它由 SNE(Stochastic Neighbor Embedding) 、对称 SNE 算法改进而来，可以说是目前数据可视化中最常用的降维算法。

3.1 原理与公式

在基本原理上，t-SNE 沿用了 SNE 与对称 SNE 的思想：将欧几里得距离转换为联合概率分布来表达点与点之间的相似度，并在低维中构建这些点的概率分布，使得低维与高维的概率分布尽可能相似。

在高维数据中，t-SNE 沿用了对称 SNE 的思路，使用高斯分布来衡量两个样本间的相似度：

而在低维，t-SNE 使用 t-分布代替高斯分布，从而能够在一定程度上减少不同簇之间的“拥挤”问题（具体原因在这里不展开介绍）。使用 t-分布后，低维空间的分布如下：

构造了高维与低维的概率分布后，就可以用 $KL$ 散度来衡量这两个分布的距离：

为了尽可能使两个分布接近，我们需要得到：

然而在数据降维中，我们有一组样本，对于整组样本求解 $KL$ 散度的全局最小是不大可能的，因此我们只能对每个 $y_i$ 使用梯度下降法进行逼近。首先求出 $y_i$ 的梯度：

根据梯度，使用一些梯度下降的算法，即可完成 t-SNE 的降维过程。

3.2 t-SNE 的算法流程

完整实现 t-SNE 算法需要以下的流程：

1. 处理高维样本 $X$ ，根据困惑度二分搜索合适的 $\sigma$
2. 对 $Y$ 进行初始化，一般可以选择随机初始化，或是使用 PCA 降维的结果作为初始条件
3. 对 $Y$ 进行梯度下降，迭代 $epoch$ 次

虽然在上面给出了公式推导，然而在 t-SNE 算法过程中，还是有许多细节。例如如何选择高斯分布的 $\sigma$ ，这里涉及到困惑度的概念，因为篇幅原因，就不展开介绍了。 sklearn 中已经实现了 t-SNE 算法：sklearn.manifold.TSNE ，可以更加方便地使用 t-SNE 对数据进行降维。

如果想要更详细地了解 SNE ，对称 SNE 以及 t-SNE 的代码实现、公式，以及 t-SNE 如何解决“拥挤”问题，可以参考 t-SNE完整笔记

4. 降维算法的比较

在上文中，其实我们主要介绍了两种截然不同的数据降维算法，一种是以 PCA （有两种实现方式）为代表的线性降维方法，而另一种是以 t-SNE 为代表的流型降维方法。在数据降维中，这两种算法均有各自的优劣。

4.1 时间复杂度

首先就是降维所需的时间，相较于 t-SNE ，PCA 算法的计算速度可谓是非常快。因为 PCA 仅仅只需要进行几步简单的线性代数运算，而 t-SNE 为了减少分布的差距，需要频繁的进行梯度下降迭代，占用大量的时间和计算资源。

4.2 数据的特征表示

因为 PCA 算法是线性算法，因此能够很好地保留数据间的向量特征，而 t-SNE 就很难做到这一点。

例如在自然语言处理的任务中，在对词向量进行适当的线性降维之后，就可以通过词向量之间的关系进行一定的词义推断。

例如，我们现在取出 man, woman, male 这三个词向量，为了直观起见，我们将它绘制于平面上。现在我们建立了 man-woman ，以及 man-male 这两个关系，现在要推断 $?$ 位置的单词是什么，如下图所示：

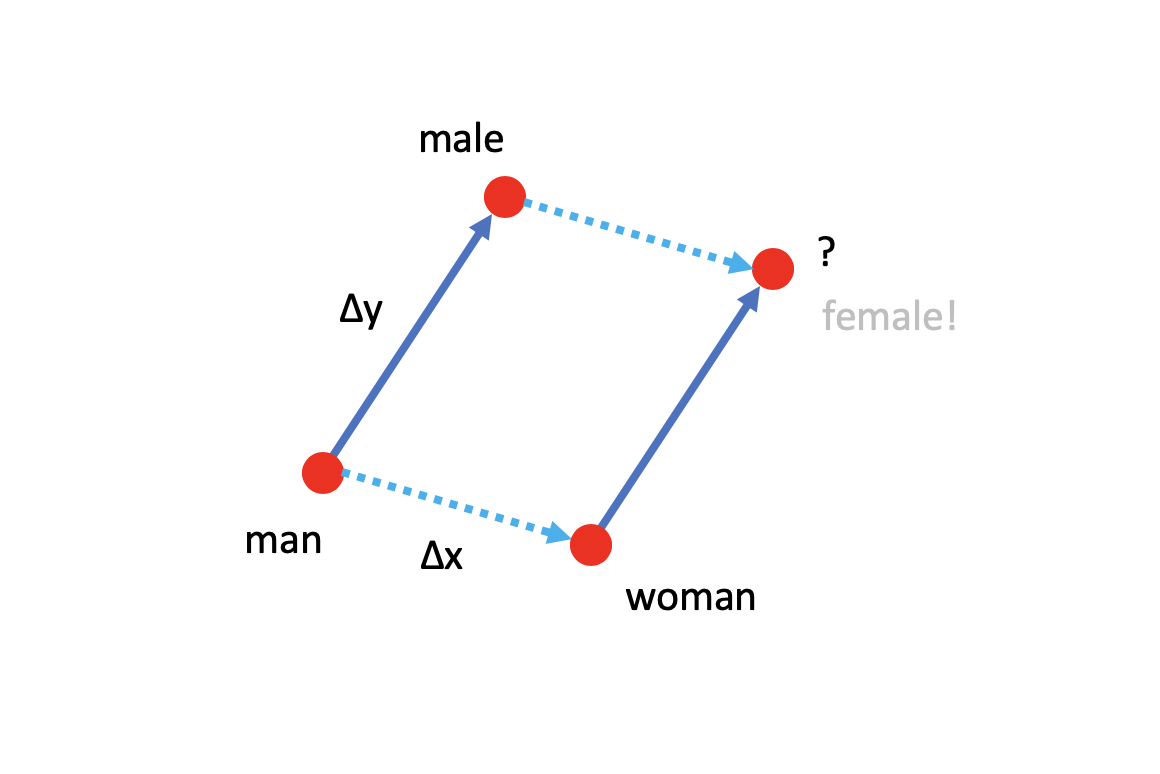
对于人类来说，我们可能很容易就知道，这个单词是 female ，而对于计算机而言可能就比较困难。此时，如果我们对词向量进行适当的线性降维，那么计算机也就能很容易发现这样类似的关系。

对于 t-SNE 来说，它只能保证数据间的相似程度（欧式距离相似），并不能保证数据间的位置关系保持不变，因此，非线性降维就不能得到这样的结果。

4.3 数据可视化

数据降维除了对数据进行压缩之外，还有一个非常重要的应用就是数据可视化。此时，我们往往会大幅压缩数据的维数，从一个极高的维度降至二、三维。此时，非线性地 t-SNE 算法就有着极大的优势。

通过非线性的映射，我们能够更好地将不同的簇在尽可能保持相似关系的情况下进行较好的分离，在可视化时就能够更加直观。

下面以 Optical Recognition of Handwritten Digits Data Set 作为测试，样本有 10 类，共 1797 个样本，每个样本的维度为 $8 \times 8 = 64$ 。

为什么不测试更为常见的 MNIST 数据集？因为 MNIST 数据集实在是太大了，训练集有 60,000 个样本，每个样本的维度为 $28 \times 28 = 784$ ，运行降维算法（尤其是 t-SNE）会花费很多时间。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.manifold import TSNE

def PCA_SVD(X, k):
    Y = X - np.mean(X, axis=1, keepdims=True)
    U, s, V = np.linalg.svd(Y)
    index = np.argsort(s)
    P = U[:,index[-k:]]
    Z = np.dot(P.T, X)

    return Z

def plot(X, y, s):
    xs = X[0,:]
    ys = X[1,:]
    s = plt.scatter(xs, ys, s=s, c=y)
    plt.legend(*s.legend_elements(), loc='upper left')

digits = load_digits()

X = np.array(digits.data)
label = digits.target

Y = PCA_SVD(X.T, 2)
plt.title('PCA')
plot(Y, label, 15)
plt.show()

Z = TSNE(n_components=2).fit_transform(X)
Z = np.array(Z).T
plt.title('t-SNE')
plot(Z, label, 12)
plt.show()

效果如下所示：

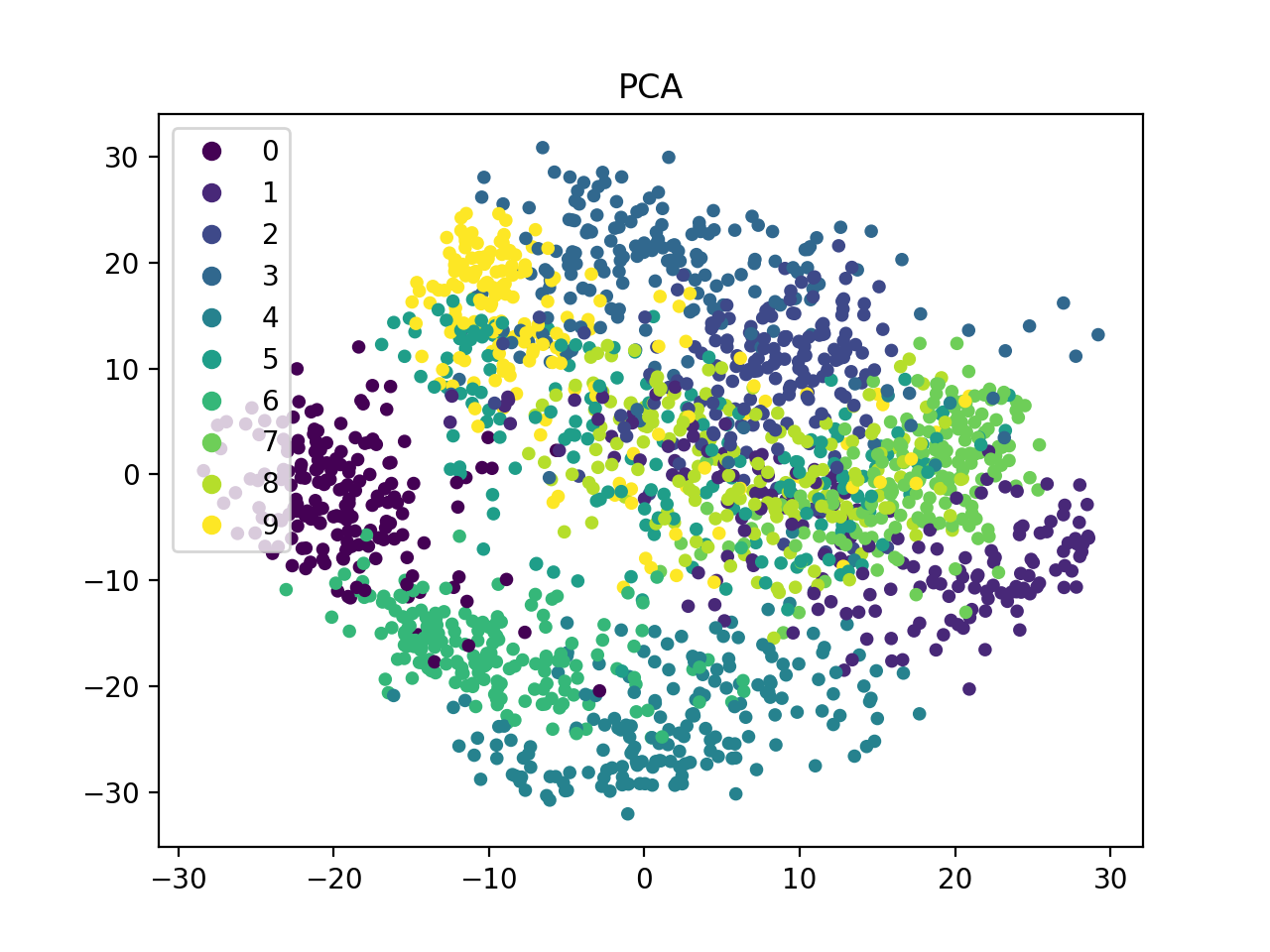
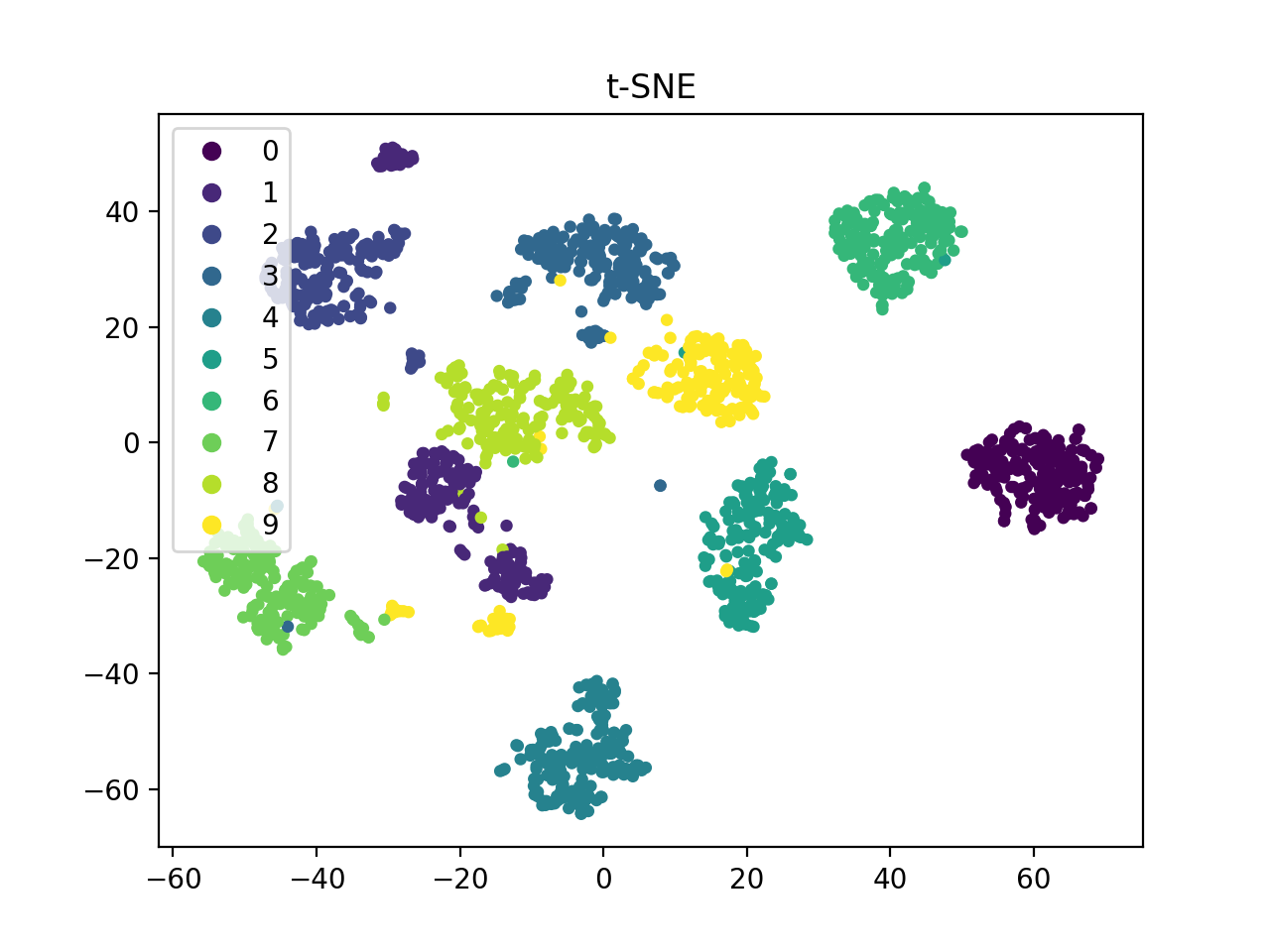
可以看到，PCA 结果中，样本的分布并不是很清晰，而 t-SNE 就能很好的展示不同簇之间的分布。

结语

在本文中，我主要介绍了 PCA 以及 t-SNE 两种常见的数据降维算法。在实践中，PCA 算法由于计算速度快，因此广泛地应用于数据压缩、模型加速、特征分析等场景；而 t-SNE 算法则普遍用于数据可视化，一般很少做其他应用。除了 PCA 和 t-SNE 外，数据降维还有许许多多其他的算法，限于篇幅，本文就不展开介绍了。