让 transformer 模型接入更长输入

Overview

注意力机制可以说是 transformer 模型中最关键的一部分，现有的 transformer 模型一般通过多头注意力（Multi-Head Attention，MHA）来捕获全局上下文之间的关系。

然而随着输入序列长度 $N$ 的增加，MHA 所需要的计算以及空间复杂度是成平方提升的，导致 transformer 模型难以处理长输入。

除了 pruning 等直接对模型大小进行裁剪的方法外，另一种主流的方案就是修改 attention 机制，从而实现在长输入下的加速。 常见的 attention 加速方法大概可以分为：设计内核，稀疏化以及“线性”attention 三种方式。

1. 设计内核（Flash Attention）

通过设计融合的 MHA 内核降低显存带宽开销

1

优点：不修改 attention 计算过程，无需重新训练。不考虑精度的情况下和原始效果一致。

缺点：需要编写底层内核，平台兼容性一般

2. Attention 稀疏化（ETC，Longformer，Big Bird）

假定在长序列中不需要建模过远的关系，主要集中在对角线位置（类似于 CNN 的滑动窗口）。对于全局 token 依旧需要与所有内容进行交互。

2

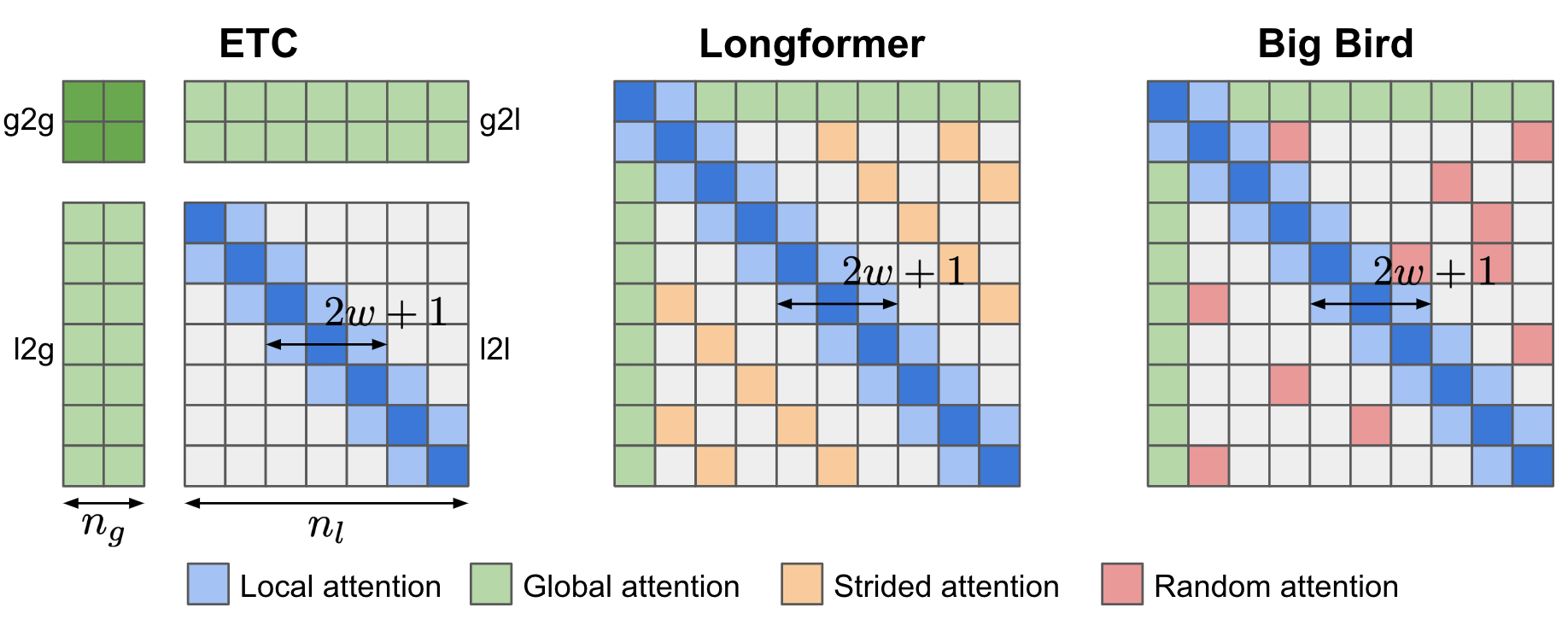
优点：设计简单，不需要引入外部模块

缺点：需要依赖稀疏矩阵运算进行实质加速，对于硬件设备以及框架有一定要求。大多数稀疏 attention 的方法会破坏原始 pretrain 模型的效果，需要进行少量 pretrain 才能恢复较好的性能。

3. “线性” Attention

3.1 基于哈希的方法（Reformer）

通过局部敏感哈希（LSH）来分组相似的 QK，并在分组后的块内进行运算

优点：通过哈希进行相关 token 的自动聚类，相较于人为设定的稀疏性具有更好的动态能力。

缺点：需要引入哈希等额外操作，并且需要编写 kernel。整体实现较为复杂，在句子长度不长时加速不明显。

3.2 基于池化的方法（Linformer）

通过在 KV 将 N 个 token 池化成 K 个 token，将 attention 复杂度从 $N^2$ 降低到 $NK$。

3

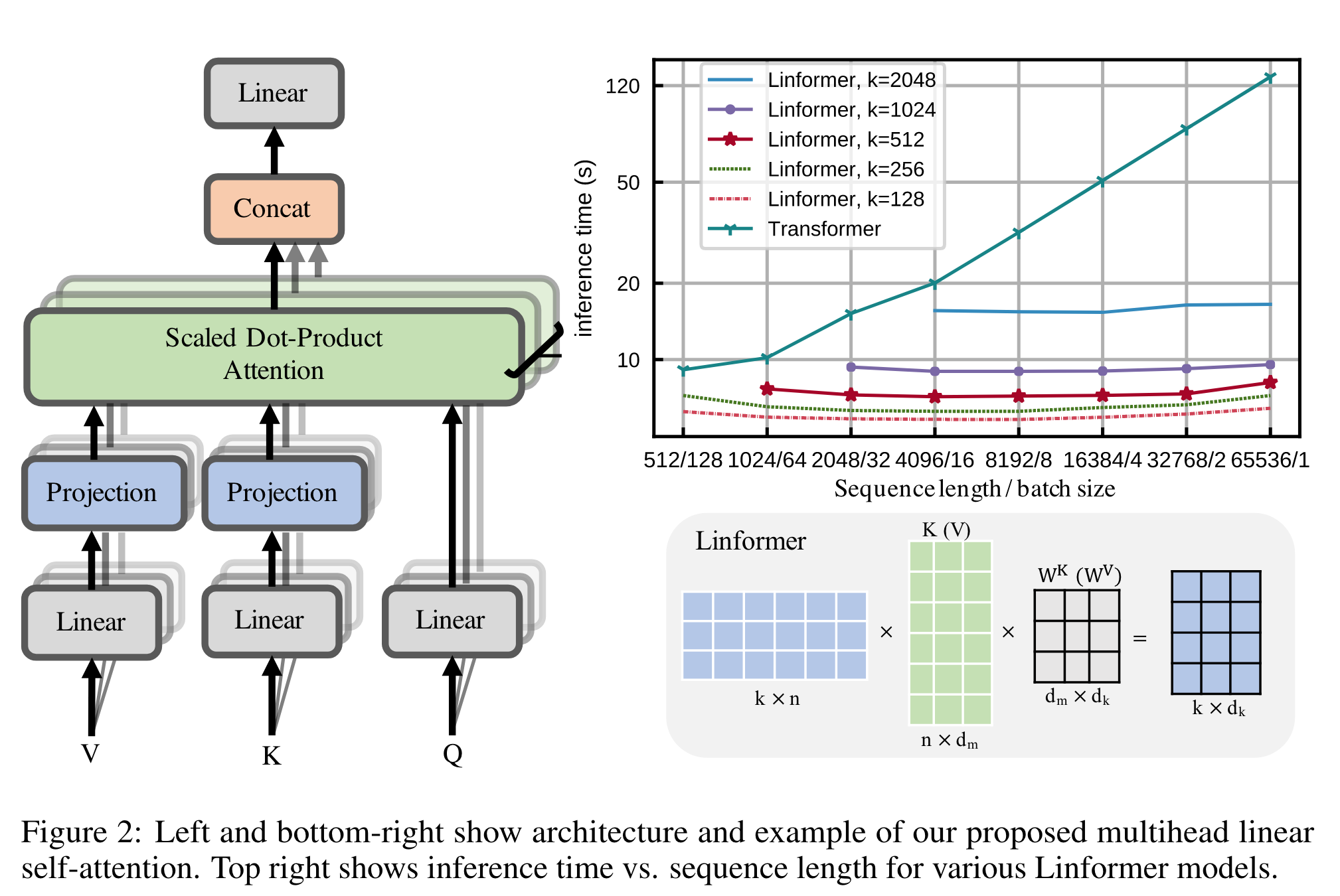
优点：实现简单，直接在 KV transform 后乘以可学习的池化矩阵即可。

缺点：建模 N->K 池化的可解释性并不强，K 的选择需要比较启发式的方法。并且池化会聚合 token 信息，导致比较难进行 mask 或者加相对位置编码等操作。

3.3 基于核函数的方法（Linear Attention，Performer）

Attention 运算中的 softmax 限制了矩阵的乘法顺序，如果通过核函数近似 softmax 相似度计算，就可以将 (QK)V 的运算顺序修改为 Q(KV)。

优点：在长文本下具有比较强的优势，可以达到近似线性的显存以及运算复杂度开销。

缺点：当序列长度与 hidden_size 接近时提升不明显。在质量评估任务上核函数近似后的表现未知，需要进行测试。

论文阅读

Longformer (Arxiv 2020)

Longformer: The Long-Document Transformer

方法

Attention Pattern

4

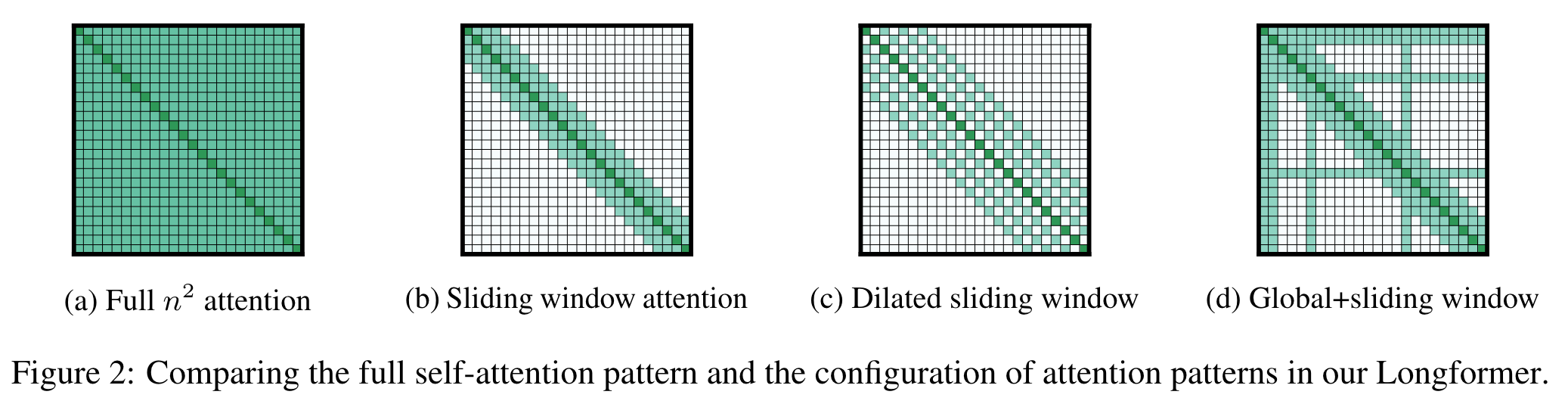
Longformer 假设在长文本下不需要过远距离的直接交互，因此可以将 Attention 的 mask 修改为沿着对角线的滑动窗口形式。全局的信息依旧可以被 CLS 捕获。

然而就像 CNN 一样，滑动窗口限制了“感受野”的大小。因此作者在每层中两个 head 引入类似于空洞卷积的窗口形式，扩大序列交互的捕捉能力。

训练

虽然 Longformer 直接采用了 RoBERTa 预训练的模型，然而直接进行输入扩长并引入滑动窗口会较大的破坏模型表现。因此还是需要进行小规模的再次预训练（65K continued MLM pretraining）。

位置编码

Longformer 采用的是 RoBERTa 作为 backbone，由于 RoBERTa 采用的是绝对位置编码，直接限制了输入长文本的能力。

Longformer 的做法是将原始的 positional embedding 复制几遍进行扩长。

结果

5

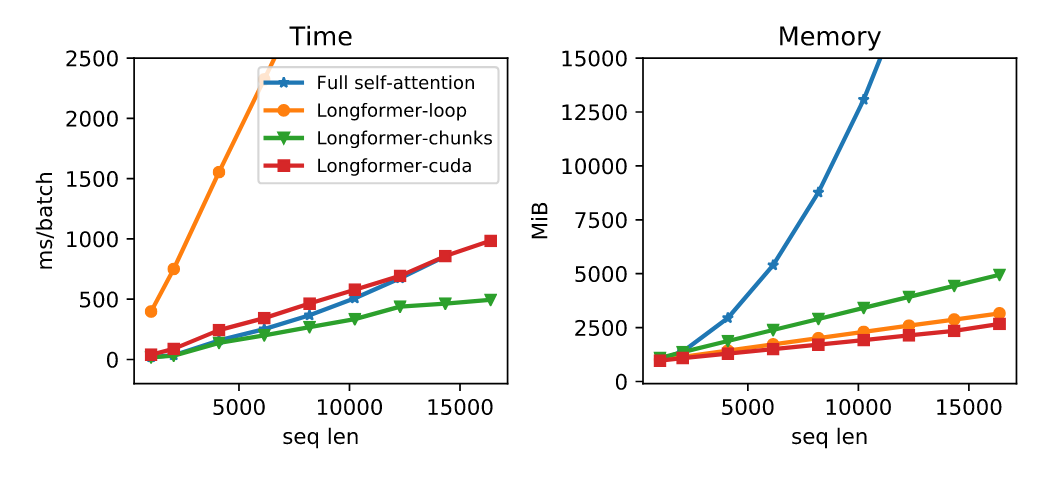
Longformer 形式可以较好的降低长文本下内存以及时间的消耗。不过时间的加速与实现方式有着比较大的关系。

6

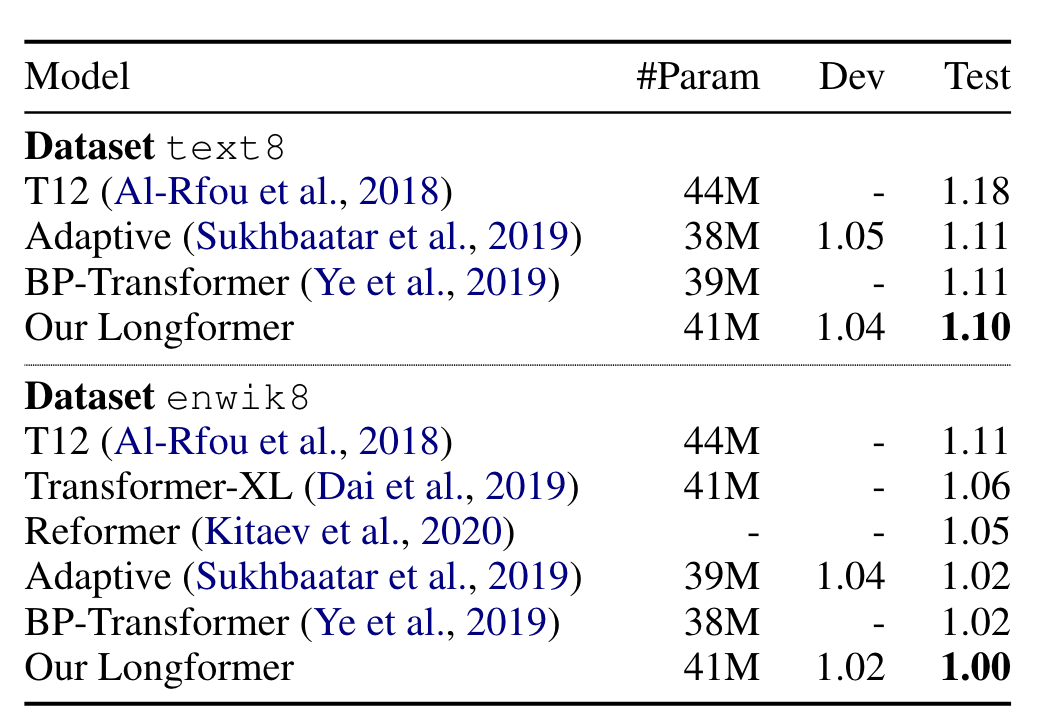
除此之外，每一层的窗口大小并不一定要一样大，作者发现窗口逐渐增大的模型效果更好，dilation 也有一定的帮助。

7

评价

Longformer 提出了一种非常简单易用的长文本 transformer 架构，能够赋予原始 RoBERTa 网络更好的长文本处理能力。

然而直接在 attention 上引入稀疏性会破坏原始预训练网络的知识，并且绝对位置编码的扩长也不是很直接，因此需要进行重新的 pretrain。并且推理加速和实现的方法有关，在某些平台上并不一定能起到比较好的加速效果。

Flash Attention (NeurIPS 2022)

FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness

方法

不保存整个 softmax attention 矩阵，而是滚动的进行计算，设计缓存友好的 attention 计算机制。由于滚动过程中前面的行和并不是最终结果，因此需要进行缩放。

例如对于数值稳定的 softmax 函数来说，形式为：

\[softmax(x) = \frac{e^{x_i-m(x)}}{\sum_{j=1}^ne^{x_j-m(x)}}\]

其中 $m(x)$ 为行最大值。此时再乘上 $V$ 矩阵就得到 attention 输出，计算公式为 $softmax(x)V$。

假设对 x 进行分块，为了简化假设 x 是长度为 4 的向量，切成左右两块 $[x_0, x_1]$, $[x_2, x_3]$，$V$ 也需要切成两个块 $V_0, V_1$ 。在计算 softmax 过程需要中维护两个值：最大值 $m$ 和指数前缀和 $l$。

在前两个块可以计算得到 $\tilde l, \tilde m$ ，此时先将 $V_0$ 乘以这个中间结果的 softmax 保存到 output 中。

\[\begin{aligned} & \tilde m = max\{x_0, x_1\} \\ & \tilde P = \exp([x_0, x_1] - \tilde m) \\ & \tilde l = rowsum(\tilde P) \\ & O = l^{-1} \tilde P V_0 \end{aligned}\]

但不难看出，此时参与计算的 $\tilde l, \tilde m$ 都不是整行的完整结果，因此在计算下一个 block 时，需要对前面带偏差的结果进行“修正”，首先修正 $m$ 和 $l$ 的值。记前一轮的结果为 $m,l$ ，修正后的结果为 $m^{new}, l^{new}$：

\[\begin{aligned} & \tilde m = max\{x_2, x_3\} \\ & \tilde P = \exp([x_2, x_3] - \tilde m) \\ & \tilde l = rowsum(\tilde P) \\ & \\ & m^{new} = max\{m,m^{new}\} \\ & l^{new} = e^{m-m^{new}}l + e^{\tilde m-m^{new}}\tilde l \end{aligned}\]

接下来要对前一轮的 $O$ 和本轮的 $P V_1$ 矩阵进行修正。首先由于最大值 $m$ 可能会更新，因此都需要乘以 $exp(m^{old} - m^{new})$。除此之外，旧的 output 是使用之前的指数和 $l$ 求得的，而现在的分母应当是 $l^{new}$，因此需要乘以 $(l^{new})^{-1}l$。

\[\begin{aligned} & O_0 = (l^{new})^{-1}le^{m-m^{new}}O \\ & O_1 = (l^{new})^{-1}e^{\tilde m-m^{new}}\tilde P V_1 \end{aligned}\]

由于矩阵乘法分块，最终的结果为两者的和，因此合并上式得：

\[O = (l^{new})^{-1}(le^{m-m^{new}}O + e^{\tilde m-m^{new}}\tilde P V_0)\]

通过不断滚动就可以在分块的情况下得到最终的 output 结果。由于 softmax 只在行上操作，因此如果将 $x$ 从向量拓展为矩阵也可以进行并行计算。

8

反向传播时可以根据 $O,m,l$ 复原出 qkv 的梯度，从而避免保存中间矩阵，节约显存开销。（而且虽然反向传播要重算，但和正向过程一样也是缓存友好的，所以比 gradient checkpointing 快）

还有个 block sparse 版本，由于计算 softmax 是分块的，可以跳过那些 masked 的块（要求 mask 也是 block 的），从而可以和 casual mask 或者稀疏 attention 方法结合，进一步加速稀疏形式 attention 的计算。

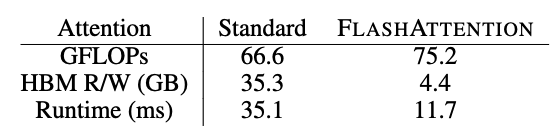
结果

理论性能分析

9

BERT 训练

10

GPT-2 模型训练

11

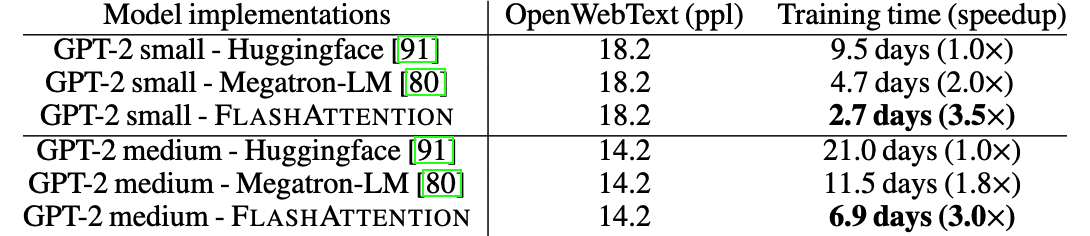
评价

后续的大模型工作中也有不少采用了 Flash Attention 机制，扩展上下文长度，例如 LLaMA，ChatGLM2 等，证明了本工作的有效性。

优点

缺点

Reformer (ICLR 2020)

Reformer: The Efficient Transformer

方法

本文提出了三种方法来改进 transformer，分别是基于局部敏感哈希（LSH）的自注意力，可逆 transformer 残差，分块 FFN。

LSH Attention

一般情况下注意力都是稀疏的，但是如何找到和最相关的 group 比较困难。作者通过局部敏感哈希（locality-sensitive hashing）来优化查找过程。

12

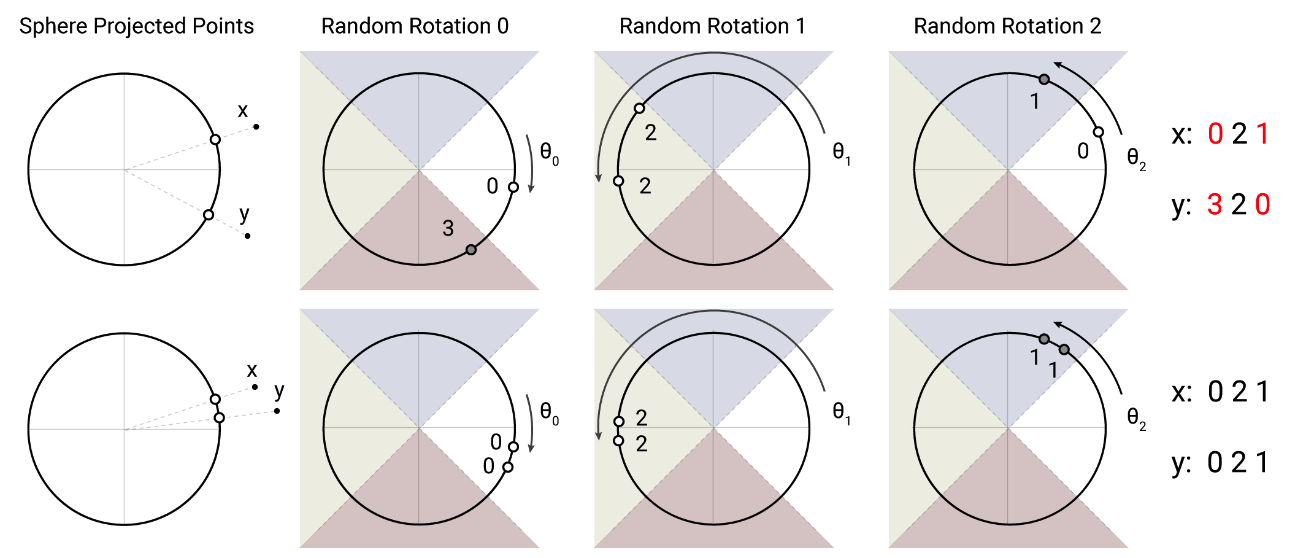
LSH 的做法是将两个点映射到超球面上，多次旋转球面，如果两个点足够接近，那么多次分类都在同一个桶里的几率就比较大。本文将 QK 都放入 LSH 中进行哈希，如果对于 self attention 就只需要 Q，复杂度 $O(L)$

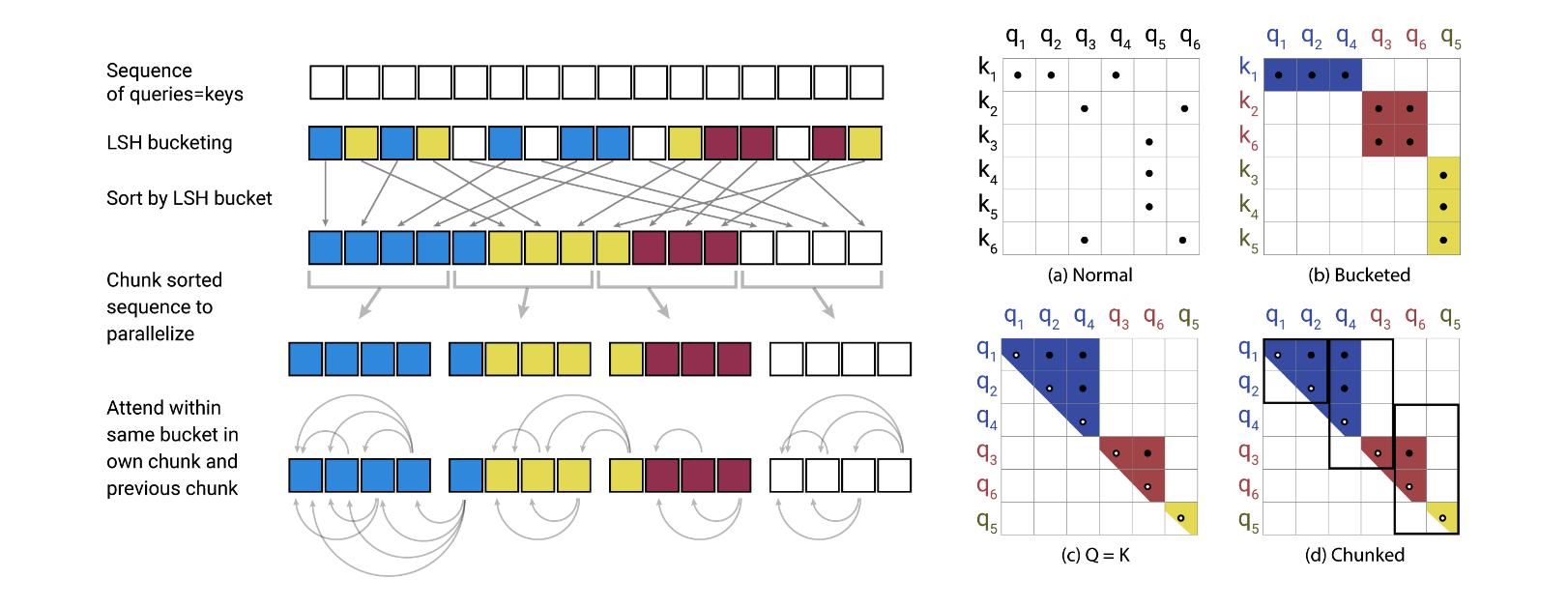
原则上这时候就可以对同一个桶内的 qk 向量进行 attention 了，但是因为哈希各个块大小不均匀，如果有个桶内元素过多，复杂度就会退化为 $O(L^2)$，因此要进行分块。

按照桶编号排序，复杂度 $O(L\log L)$。随后切成 chunk ，进行块内 attention。如果一个 chunk 的开头元素和前一个的结尾相同，则加入前一个 chunk 进行 attention（见下图 d）。这里相当于假设属于相同桶的元素个数不能超过 2 倍的块大小。这样最坏情况下每次都会关注 $m\times 2m$ 的块，对所有块完成计算的复杂度为 $O(mL)$。

13

可逆残差

由于反向传播时要保留每一层的中间结果，因此内存占用是和层数有关的。在 resnet 时就有人提出一种可逆残差网络 The Reversible Residual Network: Backpropagation Without Storing Activations，在前向时有两个 “stream” $y_1,y_2$，他们交替进行残差累加

\[y_1 = x_1 + F(x_2), y_2 = x_2 + G(y_1)\]

那么在反向传播时，就不需要知道中间结果，只需要根据 $y_1,y_2$ 进行重算就可以重新知道残差之前的值。

\[x_2 = y_2 - G(y_1), x_1 = y_1 + F(x_2)\]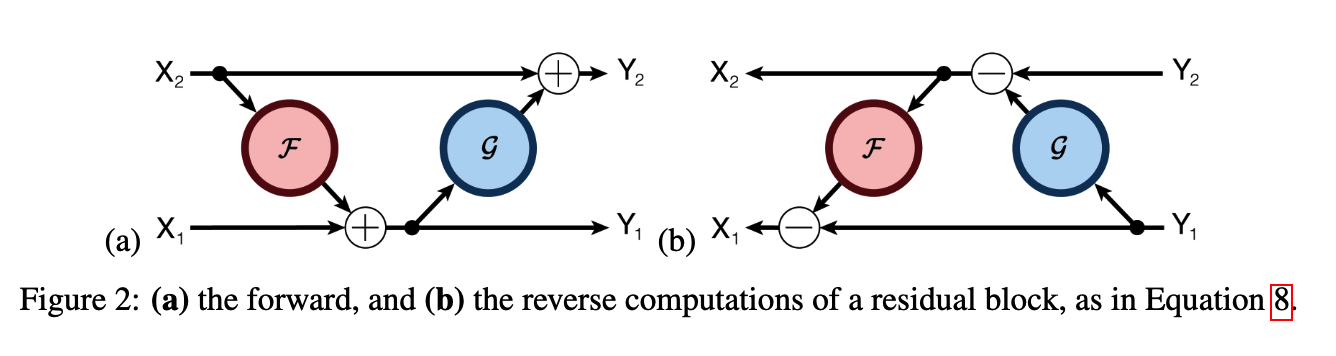

14

而在 Transformer 结构中，很明显只需要 $F$ 替换为 MHA，$G$ 替换为 FFN 就行了。此时前向不需要保留其他中间结果，显存开销和层数无关。

FFN 分块

前面已经极大减小了显存开销，但前馈过程中还有个比较花费显存的地方，就是 FFN，尤其是在中间维度一般为 $4\times dim$ 的时候。

由于 FFN 对于 (B, L) 这两个维度是没有相关性的，为了避免爆显存，在 BL 维度进行分块计算。同时也对反向传播，最终分类层做这样的处理。

评价

Linformer (arxiv 2020)

Linformer: Self-Attention with Linear Complexity

方法

通过对 $V,K$ 进行一个限定长度 $k$ 的投影来达到线性效果。

3

为了节约参数，可以选择每层共享、每个 multi-head 共享，KV 共享 Projection，最终只需要一个 $k\times n$ 的投影矩阵。

评价

个人感觉本文的方法有以下弊端：

Linear Attention (ICML20)

Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention

方法

作者认为，attention 最大的问题在于 softmax，如果将 softmax 去掉，那么就可以优先计算 KV 矩阵乘法，降低复杂度。

因此作者将原始的 attention 机制表示为广义形式（注：如果是 Causal Masking 只需要将 j=1 to N 换成 to i 即可）：

\[V_i' = \frac{\sum_{j=1}^Nsim(Q_i,K_j)V_j}{\sum_{j=1}^Nsim(Q_i,K_j)}\]

如果此时的 $sim(q,k)=\frac{e^{qk}}{\sqrt D}$ ，那么就是基于 softmax 的 attention。

如果通过核函数近似 sim 计算，那么就可以将 sim 替换为：

\[V_i' = \frac{\sum_{j=1}^N\phi(Q_i)^T\phi(K_j)V_j}{\sum_{j=1}^N\phi(Q_i)^T\phi(K_j)}\]

此时可以使用乘法结合律，优先计算 $\phi(K_j)V_j$，并且由于 $Q_i$ 与循环变量无关，可以提出循环，从而将上式优化为：

\[V_i' = \frac{\phi(Q_i)^T\sum_{j=1}^N(\phi(K_j)V_j)}{\phi(Q_i)^T\sum_{j=1}^N\phi(K_j)}\]

不难证明该计算方法具有线性复杂度。

接下来考虑核函数怎么定义。由于 sim 计算要求非负，因此可以考虑让核函数都映射到非负值域上： $k(x, y) : \mathbb{R}^{2×F} → \mathbb{R}_+$ 。作者直接给出可以采用 elu 激活函数来代表核函数（但好像没说为什么？）

\[\phi(x) = elu(x) + 1,\]

其中 $elu(x)$ 为 ReLU 的一个替代，其在负数输入上并不会直接让神经元变零，从而保留一定的梯度：

\[elu(x) = \left\{ \begin{aligned} &x & (x \ge 0) \\ &\alpha(e^x-1) & (x < 0) \\ \end{aligned} \right.\]

在反向传播时，也可以通过矩阵乘法的结合律，来得到线性的反向传播公式。

评价

本文提出的方法可以改变 QKV 的计算顺序，从而减少矩阵乘法的开销，并且不需要保留 attention 的中间结果，实现线性的时间和内存占用。

不过本方法是对原始 softmax 的一个近似，并且为何核函数选择 elu 并没有过多的解释（还有许多不同的选择方法）

Performer (ICLR 2021)

Rethinking Attention with Performers

感觉很像 [[Attention 加速#Linear Attention (ICML20)]]，将 QK 进行投影成 $Q’K’$ 后近似原来的 softmax 计算，但用的是随机变量的方式，数学不好没有看懂，先贴个链接：

Performer：用随机投影将 Attention 的复杂度线性化

总结

除了引言中说的三种分类外，从另一种角度来看，Attention 加速方案主要就是从以下两种模式入手。

  1. 从时间和空间理论复杂度层面加速。由于显存缓存等影响，降低空间复杂度的同时也能起到加速效果。
  2. 避免计算满秩（$N^2$）的注意力，将其进行池化，分解，或是只计算指定区块。

然而要注意的是，这些方案仅仅只加速了 MHA 这一个模块。对于 transformer 来说，MHA 并不一定是最耗时的。在 Compressing Large-Scale Transformer-Based Models: A Case Study on BERT 这篇论文中。作者对 BERT-base 模型进行了非常充分的分析。可以发现在输入长度只有 512 或更小的情况下，MHA 前的 QKV transform 或是最后的 FFN 所占的时间和内存都很大。苏神的这一篇文章中也阐述了一致的观点。

15

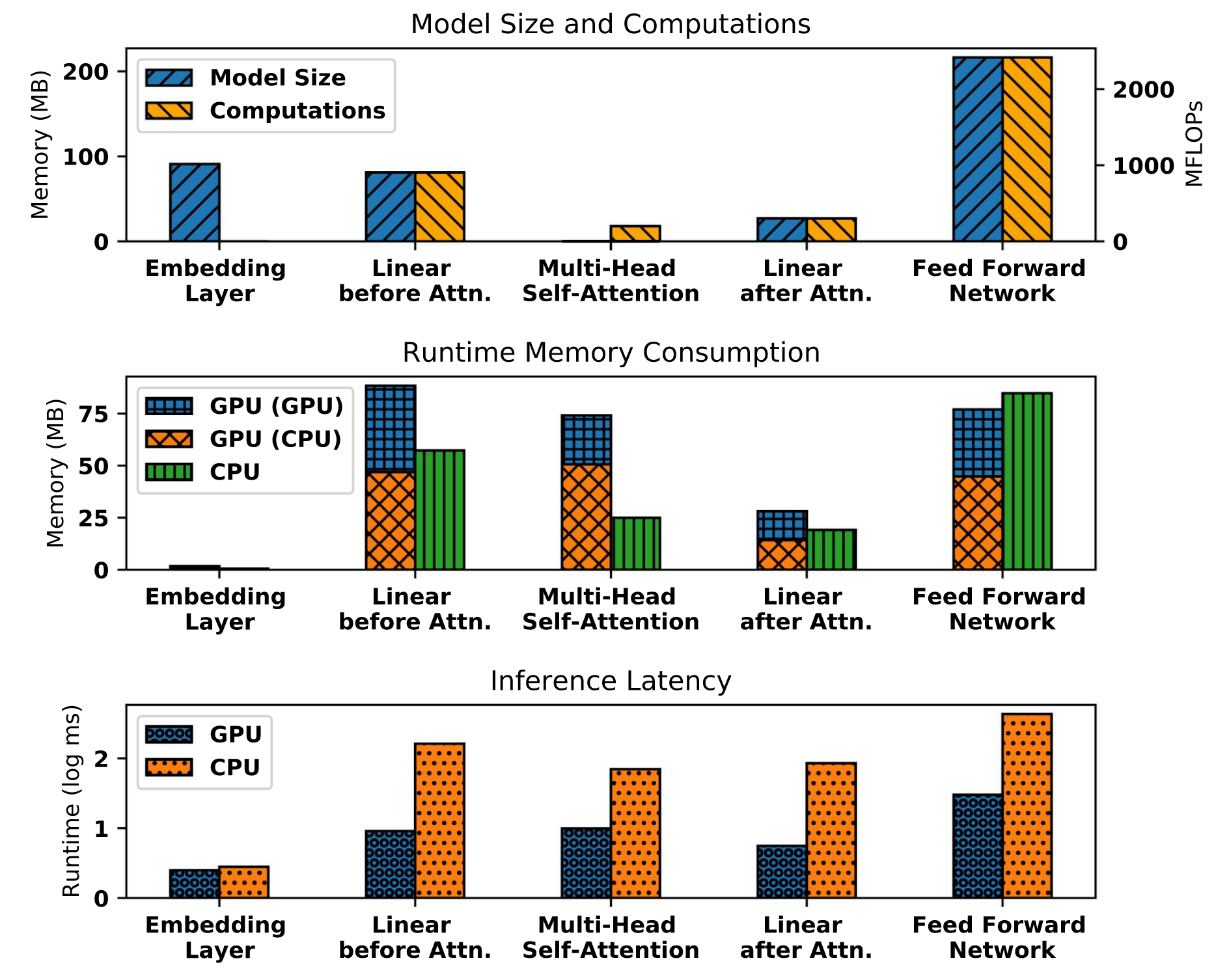
因此，上述方法往往只有在输入序列足够长时才能起到较好的加速效果。而针对 FFN 等模块也需要考虑使用正交的方法进行一同优化。

参考

感谢 Lil 大佬以及苏神对相关工作的整理以及分析，收获颇丰。

  1. The Transformer Family Version 2.0
  2. Large Transformer Model Inference Optimization
  3. 线性 Attention 的探索：Attention 必须有个 Softmax 吗？
  4. Performer：用随机投影将 Attention 的复杂度线性化
  5. 线性 Transformer 应该不是你要等的那个模型